|
|
|
Η ταινία του moebius

Για να κατασκευάσουμε την ταινία του moebius, κόβουμε από ένα φύλλο χαρτί μια ταινία όσο πλατιά θέλουμε (όχι και πολλή πλατιά) και στη συνέχεια πριν κολλήσουμε τα δύο άκρα της την περιστρέφουμε 180 μοίρες. Έτσι έχουμε κατασκευάσει αυτό που είναι γνωστό ως '' η ταινία του Moebius''.
Aς δούμε τώρα τρία πειράματα .
Αρχικά έχουμε την ταινία και στη συνέχεια ξεκινάμε να γράφουμε μια γραμμή στο μέσο του πλάτους της ταινίας και κατά μήκος της (experiment1). Τέλος κόβουμε την ταινία κατά μήκος της γραμμής και...(μπορείτε να φανταστείτε τί θα γίνει; experiment2)
Πριν δούμε το σχετικό video , θα σας περιγράψω το δεύτερο
και τρίτο πείραμα.
Πάλι έχουμε μία ταινία και αυτή τη φορά γράφουμε την γραμμή στο ένα τρίτο του πλάτους της. Κόβουμε πάλι την ταινία και ...(experiment3)
Τέλος παίρνουμε μια τρίτη ταινία και αρχικά την κόβουμε στο ένα τρίτο και στη συνέχεια το πλατύτερο κομμάτι το κόβουμε στο μέσο του πλάτους της.(experiment4)
Πάμε όμως να δούμε το σχετικό video τo οποίο θα αποκαλύψει τα αποτελέσματα των τριών πειραμάτων.
Aς δούμε τώρα τρία πειράματα .
Αρχικά έχουμε την ταινία και στη συνέχεια ξεκινάμε να γράφουμε μια γραμμή στο μέσο του πλάτους της ταινίας και κατά μήκος της (experiment1). Τέλος κόβουμε την ταινία κατά μήκος της γραμμής και...(μπορείτε να φανταστείτε τί θα γίνει; experiment2)
Πριν δούμε το σχετικό video , θα σας περιγράψω το δεύτερο
και τρίτο πείραμα.
Πάλι έχουμε μία ταινία και αυτή τη φορά γράφουμε την γραμμή στο ένα τρίτο του πλάτους της. Κόβουμε πάλι την ταινία και ...(experiment3)
Τέλος παίρνουμε μια τρίτη ταινία και αρχικά την κόβουμε στο ένα τρίτο και στη συνέχεια το πλατύτερο κομμάτι το κόβουμε στο μέσο του πλάτους της.(experiment4)
Πάμε όμως να δούμε το σχετικό video τo οποίο θα αποκαλύψει τα αποτελέσματα των τριών πειραμάτων.
|
|
Τι λέτε όμως να φτιάξουμε μία ωραία και γρήγορη κατασκευή με την ταινία του Mobius . Προτείνω , λοιπόν να δείτε το διπλανό video και να ακολουθήσετε προσεκτικά τις οδηγίες για να σας βγουν οι 2 ωραιότατες καρδούλες. Καλό είναι να χρησιμοποιήσετε χαρτόνι αντί για χαρτί. Καλή διασκέδαση.
|
Πάνω στην ταινία του Moebius βασίζεται και η λύση ενός γνωστού γρίφου, που μπορείτε να δείτε εδώ.
August Ferdinand Moebius (1790-1868)

O August Ferdinand Moebius ήταν ένας Γερμανός μαθηματικός , που διέπρεψε στην ολοκλήρωση σημαντικών έργων στο πεδίο γενικά της Γεωμετρίας. Ο ίδιος, ωστόσο, έγινε εξαιρετικά δημοφιλής, πέρα από το επιστημονικό επίπεδο, χάρη στην ευρηματική ανακάλυψη που σήμαινε η ταινία που φέρει το ονομά του. Λέγεται συνήθως ότι η δημιουργική ικανότητα των επιστημόνων , ιδιαίτερα των μαθηματικών , φτάνει στο απόγειο της κατά τα πρώτα χρόνια της νεότητας και ότι χρησιμοποιούν την ωριμότητα για να τελειοποιήσουν τα πρώτα και πρωτότυπα ευρήματά τους . Ο Moebius αποτελεί μια ξεκάθαρη εξαίρεση αυτού που μόλις προαναφέραμε , αφού δημιούργησε από ένα διδιάστατο αντικείμενο ( το φύλλο χαρτί) ένα τριδιάστατο (την ταινία ) χωρίς να την μεταβάλη σε ηλικία 68 χρονών.
Το ενδιαφέρον που προκάλεσε η ταινία του Moebius υπερέβη το καθαρά μαθηματικό πλαίσιο και βρήκε ενδιαφέρουσες βιομηχανικές και τεχνικές εφαρμογές , οι οποίες αποτέλεσαν αφετηρία για περισσότερες από δέκα πατέντες , όπως για παράδειγμα μια ταινία που μπορεί να εγγραφεί και από τις δύο πλευρές , ανακάλυψη που εφαρμόστηκε και στις μαγνητοταινίες , ταινίες μεταφοράς που υπόκεινται στη μισή από την αναμενόμενη φθορά ή ταινίες λειαντικού υλικού που αντέχουν το διπλάσιο από τις συμβατικές.
(Πηγή : Παιχνίδια ευφυ'ι'ας , De AGOSTINI )
Το ενδιαφέρον που προκάλεσε η ταινία του Moebius υπερέβη το καθαρά μαθηματικό πλαίσιο και βρήκε ενδιαφέρουσες βιομηχανικές και τεχνικές εφαρμογές , οι οποίες αποτέλεσαν αφετηρία για περισσότερες από δέκα πατέντες , όπως για παράδειγμα μια ταινία που μπορεί να εγγραφεί και από τις δύο πλευρές , ανακάλυψη που εφαρμόστηκε και στις μαγνητοταινίες , ταινίες μεταφοράς που υπόκεινται στη μισή από την αναμενόμενη φθορά ή ταινίες λειαντικού υλικού που αντέχουν το διπλάσιο από τις συμβατικές.
(Πηγή : Παιχνίδια ευφυ'ι'ας , De AGOSTINI )
Maurits Cornelis Escher (1898-1972)
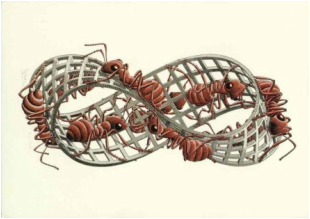
Μια τόσο πρωτότυπη και γεμάτη φαντασία αναπαράσταση της ταινίας του Moebius , όπως αυτή που αναπαράγει αυτή η εικόνα , θα μπορούσε να είναι μόνο ιδέα ενός καλλιτέχνη του βεληνεκούς του Ολλανδού Maurits Cornelis Escher. Ο Escher ήταν προικισμένος με μια εκπληκτική ικανότητα να φαντάζεται και να αναπαριστά τις πιο πολύπλοκες σχέσεις χώρου , πράγμα που του επέστρεψε να δημιουργήσει κατά τη διάρκεια της ζωής του ένα γραφικό έργο γεμάτο εικόνες που βάζουν συνεχώς σε δοκιμασία την ικανότητα αντίληψης του θεατή . Εδώ μπορείτε να θαυμάσετε μερικά από τα εκπληκτικά σχέδιά του , που πραγματικά ακροβατούν μεταξύ της λογικής και της οφθαλμαπάτης.
(Πηγή : Παιχνίδια ευφυ'ι'ας , De AGOSTINI )
(Πηγή : Παιχνίδια ευφυ'ι'ας , De AGOSTINI )
Felix Klein (1849-1925)

Όπως η διδιάστατη ταινία υπέστει την μετατροπή του Moebius και προέκυψε η τριδιάστατη ταινία του Moebius έτσι και αυτή με την σειρά της αν υποστεί την τοπολογική μετατροπή του Klein τότε προκύπτει η τετραδιάστατη κατασκευή ''Η φιάλη του Klein''.
Η φιάλη που δημιούργησε ο Γερμανός μαθηματικός Felix Klein είναι το αποτέλεσμα μιας άσκησης << μαθηματικής παπυροφλεξίας >>.
Μπορούμε να κατασκευάσουμε θεωρητικά μια φιάλη του Klein αν πάρουμε μια μακριά λωρίδα χαρτιού και ενώσουμε τις μεγάλες άκρες της , φτιάχνοντας με αυτόν τον τρόπο έναν κύλινδρο. Στην συνέχεια χρειάζεται να κάνουμε το ταχυδακτυλουρικό σε μια ανώτερη διάσταση. Αυτό που κάνουμε είναι ότι εισάγουμε το ένα άκρο του κυλίνδρου στο σώμα του,(χωρίς αυτό να κοπεί!!!) και ενώνουμε τα δύο άκρα της . Ένα από τα πολλά θαυμαστά αυτής της φιάλης , πέρα από τις ενδιαφέρουσες τοπολογικές της ιδιότητες , είναι ότι δεν μπορεί ποτέ να γεμίσει , αφού αρχίζει να αδειάζει καθώς γεμίζει. Τέλος αν μπορούσαμε να κόψουμε την φιάλη του Klein στο πλάι τότε θα προέκυπτε η ταινία του Moebius, δείτε το παρακάτω video το οποίο είναι άκρως κατατοπιστικό.
(Πηγή : Παιχνίδια ευφυ'ι'ας , De AGOSTINI )
Η φιάλη που δημιούργησε ο Γερμανός μαθηματικός Felix Klein είναι το αποτέλεσμα μιας άσκησης << μαθηματικής παπυροφλεξίας >>.
Μπορούμε να κατασκευάσουμε θεωρητικά μια φιάλη του Klein αν πάρουμε μια μακριά λωρίδα χαρτιού και ενώσουμε τις μεγάλες άκρες της , φτιάχνοντας με αυτόν τον τρόπο έναν κύλινδρο. Στην συνέχεια χρειάζεται να κάνουμε το ταχυδακτυλουρικό σε μια ανώτερη διάσταση. Αυτό που κάνουμε είναι ότι εισάγουμε το ένα άκρο του κυλίνδρου στο σώμα του,(χωρίς αυτό να κοπεί!!!) και ενώνουμε τα δύο άκρα της . Ένα από τα πολλά θαυμαστά αυτής της φιάλης , πέρα από τις ενδιαφέρουσες τοπολογικές της ιδιότητες , είναι ότι δεν μπορεί ποτέ να γεμίσει , αφού αρχίζει να αδειάζει καθώς γεμίζει. Τέλος αν μπορούσαμε να κόψουμε την φιάλη του Klein στο πλάι τότε θα προέκυπτε η ταινία του Moebius, δείτε το παρακάτω video το οποίο είναι άκρως κατατοπιστικό.
(Πηγή : Παιχνίδια ευφυ'ι'ας , De AGOSTINI )
