Ζωγραφίζοντας με κύκλους
Τι λέτε να ζωγραφίσουμε εντυπωσιακά σχέδια με τη βοήθεια περιστρεφόμενων κύκλων και γιατί όχι να τα εκτυπώσετε και να διακοσμήσετε είτε τα τετράδια σας είτε το δωμάτιό σας. Όπως είναι φυσικό αυτή η δραστηριότητα θα αποτελέσει μία καλή ευκαιρία για να γνωρίσουμε τον κύκλο και τις ιδιότητές του και όχι μόνο...Τα υπόλοιπα Μαθηματικά τα αφήνω για έκπληξη. Η ιστοσελίδα που φιλοξενεί την δραστηριότητα είναι η www.mathplayground.com.
|
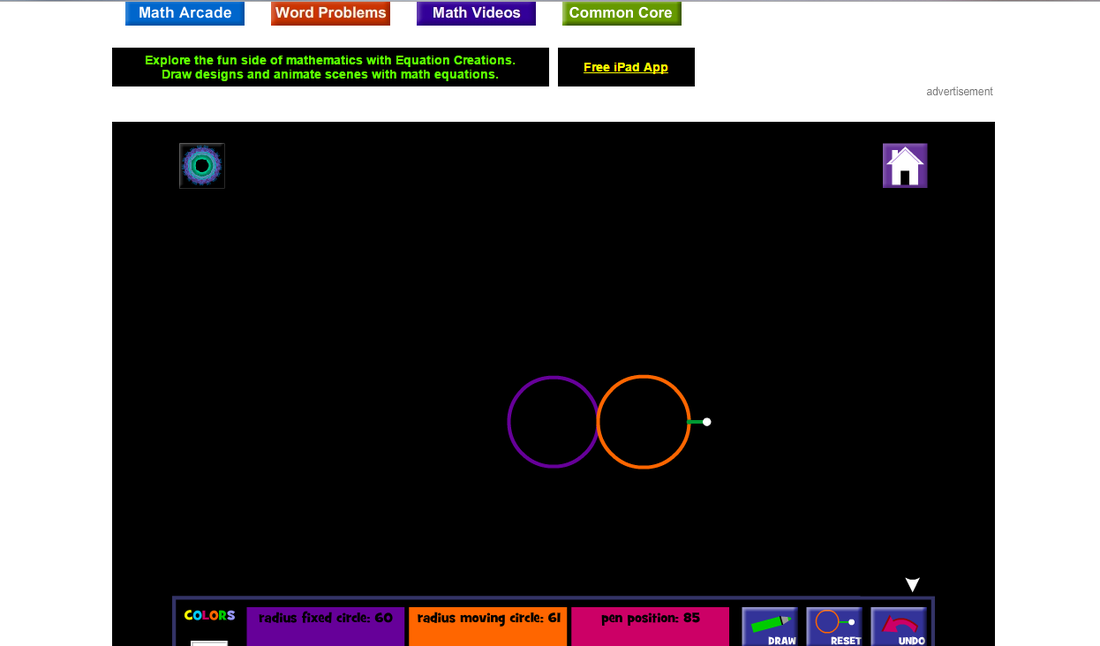
Κάντε κλικ εδώ και θα δείτε τη διπλανή εικόνα ....
Λογικά τώρα θα έχετε μπροστά σας το περιβάλλον που θα εργαστείτε , οπότε είστε έτοιμοι για να δημιουργήσετε τα μοτίβα που θέλετε.
|
|
Πριν ξεκινήσετε αυξομειώστε τις ακτίνες των 2 κύκλων , αλλά και το μήκος της γραφίδας. Μια μικρή αλλαγή στα 3 μήκη δημιουργεί εντυπωσιακές μεταβολές στο σχέδιο.
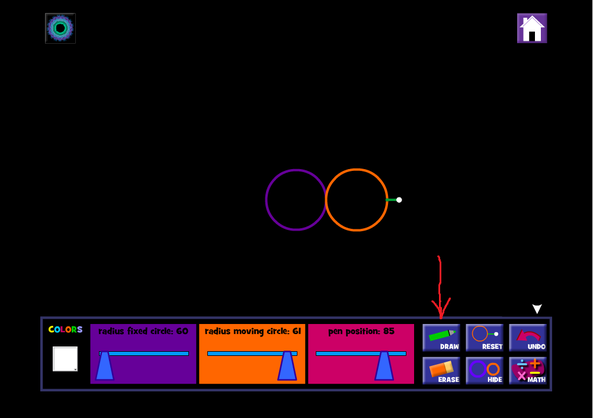
Τώρα δεν έχετε παρά να πειραματιστείτε , γι' αυτό πατήστε το εικονίδιο που έχει το κόκκινο βέλος. Ο μοβ κύκλος θα παραμείνει σταθερός και ο πορτοκαλή κύκλος θα γυρίζει γύρω από αυτόν . Αν ξανά πατήσετε το ίδιο εικονίδιο η κίνηση σταματάει . Σταματώντας την κίνηση έχετε τη δυνατότητα να να αλλάξετε το χρώμα της γραφίδας (βλέπε το κόκκινο βέλος) και να κάνετε το σχήμα εντυπωσιακότερο. Μόλις αλλάξετε το χρώμα πατάτε ξανά το εικονίδιο με το μολύβι και η κίνηση ξανά αρχίζει.
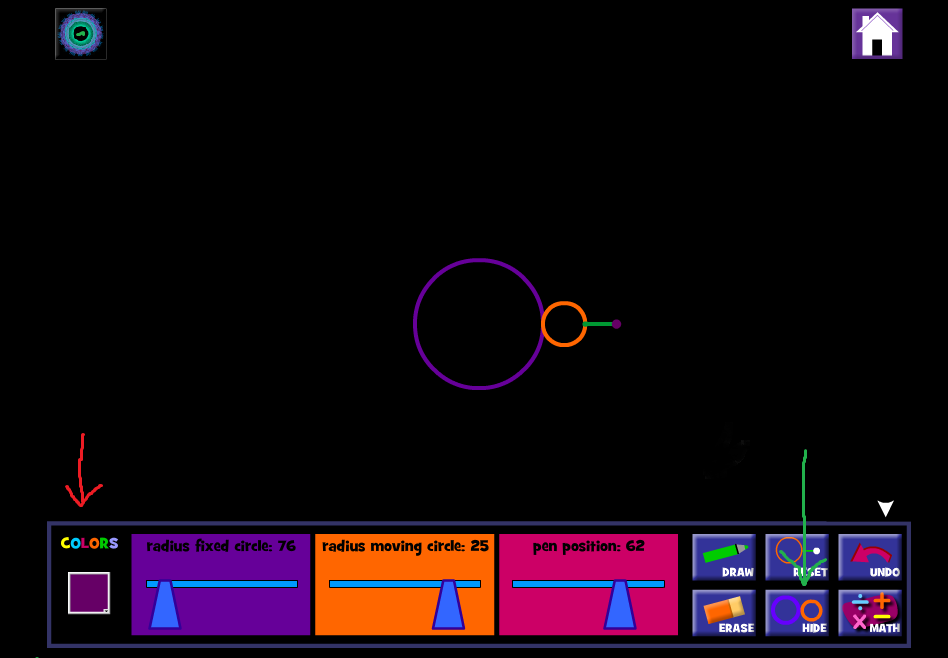
Έχω ανεβάσει παραδείγματα πολύχρωμων μοτίβων, οπότε νομίζω ότι καταλαβαίνετε τι εννοώ. Τελειώνοντας μπορείτε να κρύψετε τους κύκλους ( βλέπε το πράσινο βέλος ) και η ζωγραφιά είναι έτοιμη. Η δραστηριότητα αυτή μπορεί να συνδυαστεί με την εφαρμογή paint (ζωγραφική ) και να αποθηκεύσετε τα σχέδια στον Η/Υ ως εικόνες. Καλή διασκέδαση , περιμένω σχόλια και σχέδια που φτιάξατε εδώ. Παρακάτω έχετε τη δυνατότητα να δείτε μερικές δημιουργίες, μετά από πειραματισμούς, που έκανα εγώ και ο γιος μου. |
Κάντε κλικ πάνω στις εικόνες και θα μεγεθυνθούν. Σε μερικά σχέδια υπάρχουν και οι ρυθμίσεις για να τις δημιουργήσετε και εσείς.
Καλά διασκεδάσετε τώρα, νομίζω όμως ότι είναι ώρα για να δούμε και τα Μαθηματικά που κρύβονται πίσω από τα μοτίβα αυτά.
|
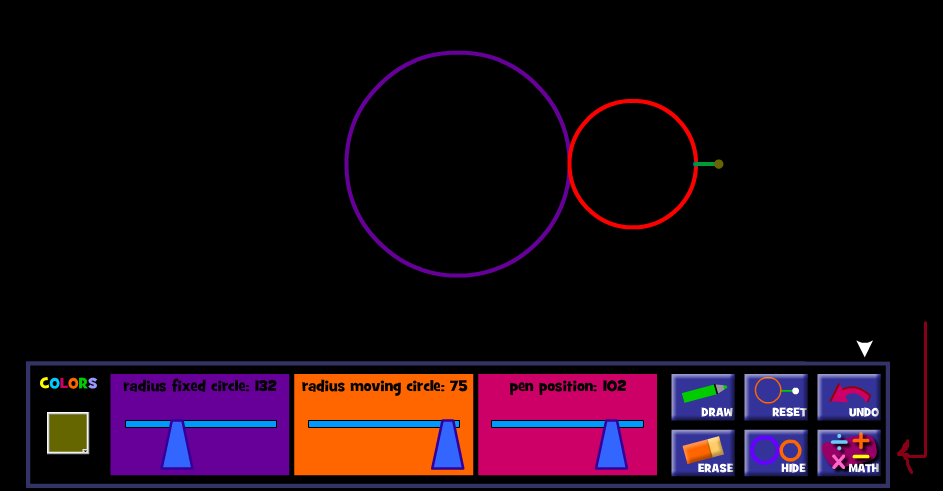
Πατήστε το τετράγωνο που δείχνει το βελάκι στη διπλανή εικόνα και θα δείτε το παρακάτω περιβάλλον :
Το ταξίδι στη Μαθηματική γνώση μόλις αρχίζει. Μην ανησυχείτε θα είναι σύντομο , περιεκτικό και αρκετά ενδιαφέρον για όλα τα Μαθηματικά γούστα. Όπως βλέπετε ξεκινάει με τους απλούς ορισμούς και βήμα βήμα σας οδηγεί σε ολοένα πιο απαιτητικές Μαθηματικές έννοιες.
|
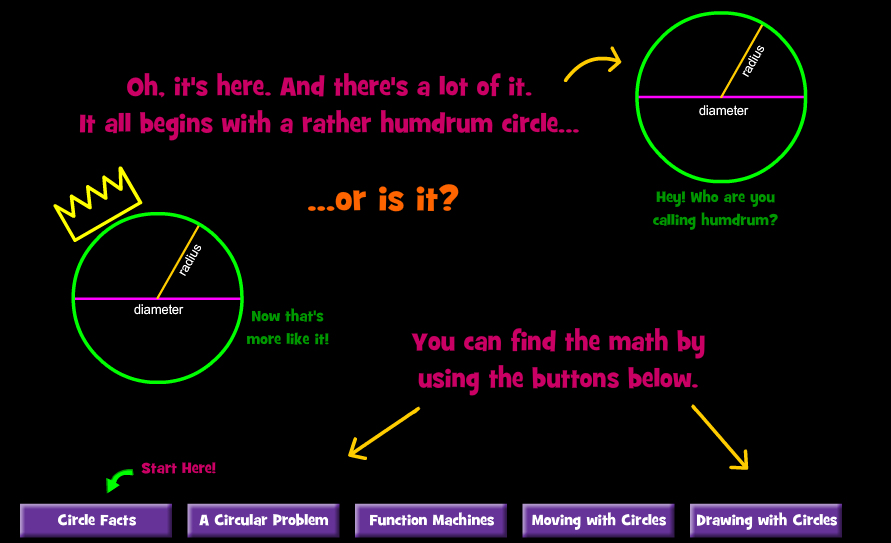
Πατήστε το ορθογώνιο κάτω αριστερά << Circle Facts>> εκεί που λέει Start Here και θα δείτε την παρακάτω εικόνα.
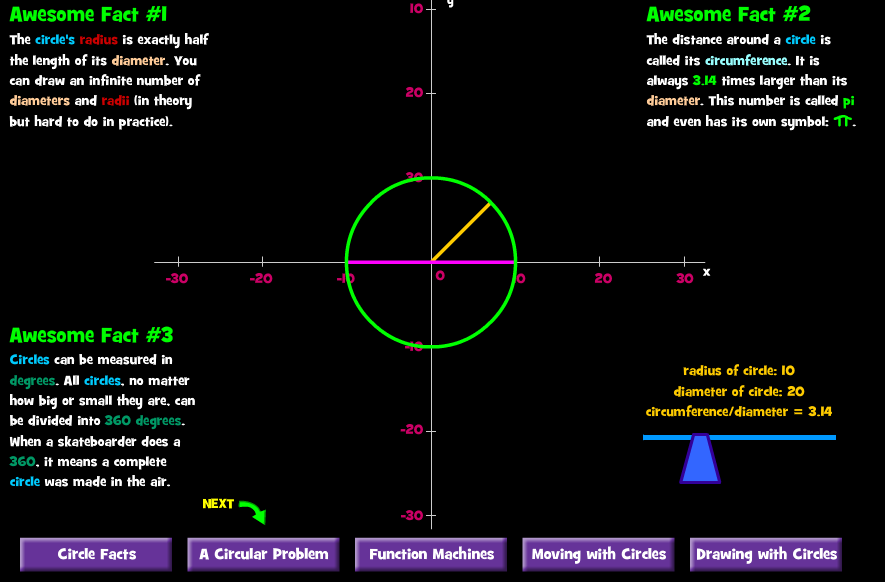
Έτσι λοιπόν περνάμε σε πιο αναλυτικούς ορισμούς, της ακτίνας, της διαμέτρου και της σχέσης τους: διάμετρος=2χ(ακτίνα) , στην περιμέτρο του κύκλου, τον αριθμό π αλλά και στο μέτρο του κύκλου ως τόξο. Κάτω δεξιά (μπλε δρομέας) έχετε τη δυνατότητα να αυξομειώσετε την ακτίνα του κύκλου και να διαπιστώσετε ότι <<ο λόγος της Περιμέτρου ενός κύκλου ως προς την διάμετρό του είναι πάντα σταθερός και ίσος με τον ''μαγικό'' αριθμό π>>. Πατώντας το επόμενο ορθογώνιο ( ΝΕΧΤ ) << A Circular Problem>> , θα δείτε το παρακάτω περιβάλλον :
Εδώ , μπορείτε να κινήσετε το πορτοκαλί τετράγωνο και να δείτε τις συντεταγμένες 4ων γνωστών σημείων , μπορείτε να τις βρείτε;
Για τα υπόλοιπα σημεία τι γίνεται , δεν μπορούμε να υπολογίσουμε τις συντεταγμένες τους ;
Με αφορμή αυτόν τον προβληματισμό συνδέουμε τη γωνία που σχηματίζουν η ακτίνα του κύκλου και ο θετικός ημιάξονας των χ , με τις συντεταγμένες του σημείου. Ουσιαστικά περνάμε στην περιοχή της Τριγωνομετρίας. Πάμε λοιπόν λίγο παρακάτω πατώντας πατώντας το επόμενο ορθογώνιο ( Ok, but how???) << Function Machines>> , θα δείτε το παρακάτω περιβάλλον :
Για τα υπόλοιπα σημεία τι γίνεται , δεν μπορούμε να υπολογίσουμε τις συντεταγμένες τους ;
Με αφορμή αυτόν τον προβληματισμό συνδέουμε τη γωνία που σχηματίζουν η ακτίνα του κύκλου και ο θετικός ημιάξονας των χ , με τις συντεταγμένες του σημείου. Ουσιαστικά περνάμε στην περιοχή της Τριγωνομετρίας. Πάμε λοιπόν λίγο παρακάτω πατώντας πατώντας το επόμενο ορθογώνιο ( Ok, but how???) << Function Machines>> , θα δείτε το παρακάτω περιβάλλον :
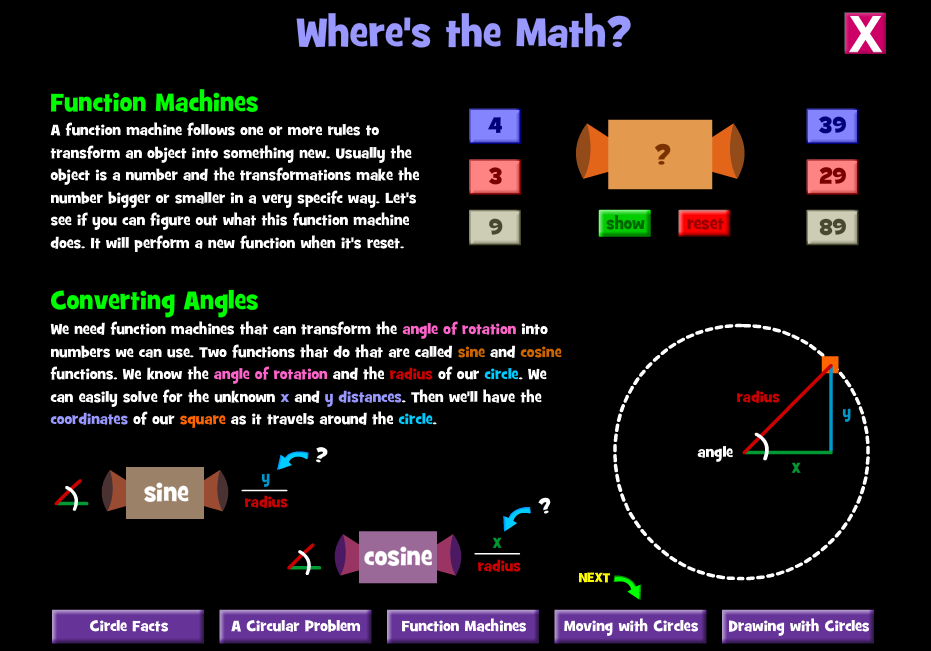
Λοιπόν εδώ έχει μία ενδιαφέρουσα εφαρμογή , ώστε οι μαθητές να εξοικειωθούν με την έννοια της συνάρτησης ( Function Machines ).
Άντε να σας βοηθήσω λίγο , πάνω δεξιά βλέπετε δύο στήλες από 3 αριθμούς , πρέπει να λοιπόν να μαντέψετε με ποιον τρόπο :
το 4 έγινε 39
το 3 έγινε 29 και
το 9 έγινε 89
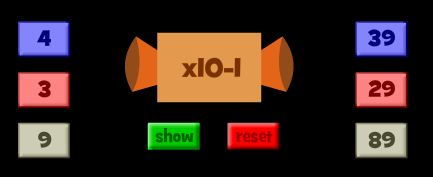
Αν δεν μπορείτε να βρείτε τη συνάρτηση πατάτε το <<show>> και σας δείχνει :
Άντε να σας βοηθήσω λίγο , πάνω δεξιά βλέπετε δύο στήλες από 3 αριθμούς , πρέπει να λοιπόν να μαντέψετε με ποιον τρόπο :
το 4 έγινε 39
το 3 έγινε 29 και
το 9 έγινε 89
Αν δεν μπορείτε να βρείτε τη συνάρτηση πατάτε το <<show>> και σας δείχνει :
Πατώντας το << reset>> έχετε όσες προσπάθειες θέλετε με άλλα τρία ζεύγη αριθμών , όρεξη να έχετε να σκέφτεστε.
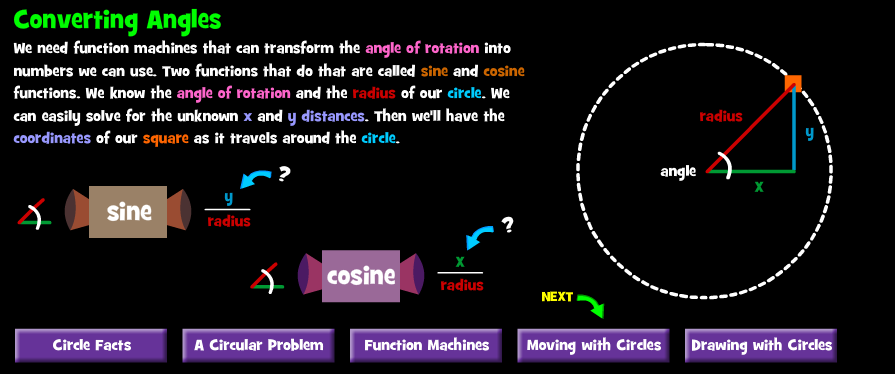
Αφού γνωρίσετε την έννοια της συνάρτησης, στη συνέχεια θα δείτε τους τριγωνομετρικούς αριθμούς ημίτονο (ημφ=sinφ) και συνημίτονο(συνφ=cosφ) μιας γωνίας φ καθώς και τη σχέση που τους συνδέει με τις συντεταγμένες του αντίστοιχου σημείου ( πορτοκαλί τετραγωνάκι).
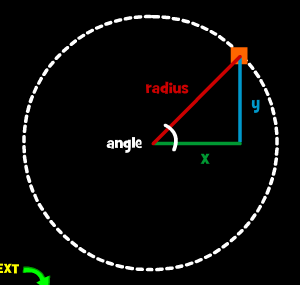
Πιο συγκεκριμένα , γνωρίζοντας τις τιμές των sine , cosine και έχοντας γνωστή την ακτίνα (radius) μπορούμε από τους πιο κάτω τύπους να βρούμε τις συντεταγμένες (χ,y) , οποιουδήποτε σημείου που αντιστοιχεί στη γωνία ( angle). Οι τιμές των sine , cosine είναι γνωστές για όλες τις γωνίες.
Ρίχτε μια ματιά εδώ.
Αφού γνωρίσετε την έννοια της συνάρτησης, στη συνέχεια θα δείτε τους τριγωνομετρικούς αριθμούς ημίτονο (ημφ=sinφ) και συνημίτονο(συνφ=cosφ) μιας γωνίας φ καθώς και τη σχέση που τους συνδέει με τις συντεταγμένες του αντίστοιχου σημείου ( πορτοκαλί τετραγωνάκι).
Πιο συγκεκριμένα , γνωρίζοντας τις τιμές των sine , cosine και έχοντας γνωστή την ακτίνα (radius) μπορούμε από τους πιο κάτω τύπους να βρούμε τις συντεταγμένες (χ,y) , οποιουδήποτε σημείου που αντιστοιχεί στη γωνία ( angle). Οι τιμές των sine , cosine είναι γνωστές για όλες τις γωνίες.
Ρίχτε μια ματιά εδώ.
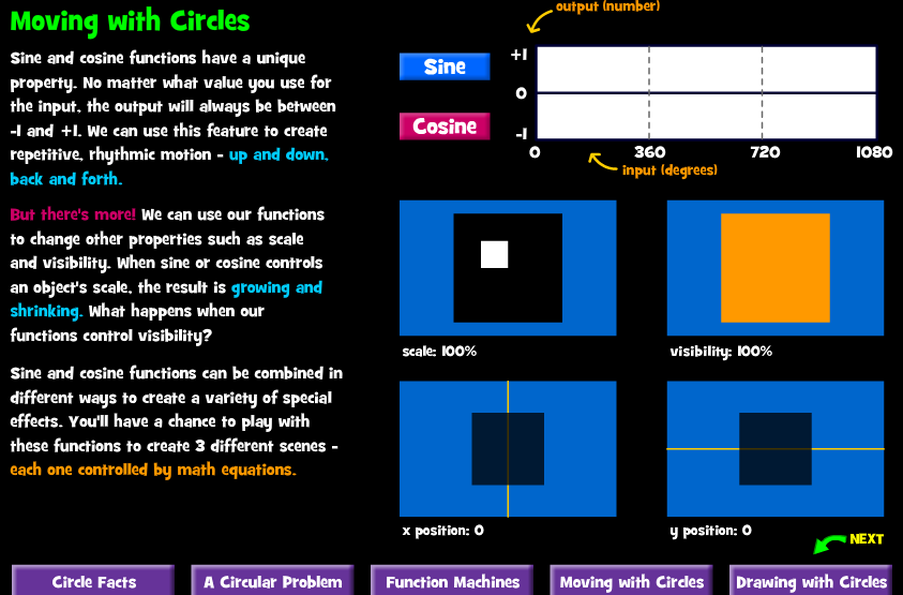
Τι λέτε να το δυσκολέψουμε λίγο; Πατήστε εκεί που δείχνει το πράσινο βέλος ( Moving with Circles) και πάμε να δούμε την τελευταία ενότητα , που είναι η γραφική παράσταση των τριγωνομετρικών συναρτήσεων του ημιτόνου (sine) και του συνημιτόνου ( cosine). Ουσιαστικά συνδέει τις τιμές των 2 τριγωνομετρικών αριθμών με τις αντίστοιχες γωνίες ( από 0 μοίρες έως 1080 μοίρες). Βλέποντας την πιο κάτω εικόνα:
Πατήστε μία φορά το μπλε τετράγωνο sine για να δείτε πως είναι η γραφική του παράσταση και μετά κάντε το ίδιο με το μοβ για το cosine. Η περιοδικότητα του φαινομένου είναι χαρακτηριστική , συσχετίστε την κίνηση των παρακάτω σχημάτων με την κάθε μία συνάρτηση και δείτε την απόλυτη αρμονία που έχουν μεταξύ τους. Προφανώς τα Μαθηματικά υπάρχουν παντού πόσο μάλλον και στα γραφικά των Η/Υ.
Μια ωραία εφαρμογή ,που έχω φτιάξει με το λογισμικό GEOGEBRA, είναι η παρακάτω. Ουσιαστικά συνδέει το μέτρο μιας γωνίας ( ακτίνια=rad) με τους τριγωνομετρικούς αριθμούς ημίτονο και συνημίτονο και βλέπουμε την γραφική τους παράσταση. Για μεγαλύτερα παιδιά ( Β΄λυκείου ) μπορείτε να δείτε ένα ενδιαφέρον φύλλο εργασίας εδώ σχετικά με τις τριγωνομετρικές συναρτήσεις. Για να δείτε την εφαρμογή κινήστε το σημείο Ε . Στη συνέχεια κάντε ένα ένα κλικ στα 2 πρώτα τετραγωνάκια Συνημίτονο γωνίας -Ημίτονο γωνίας.
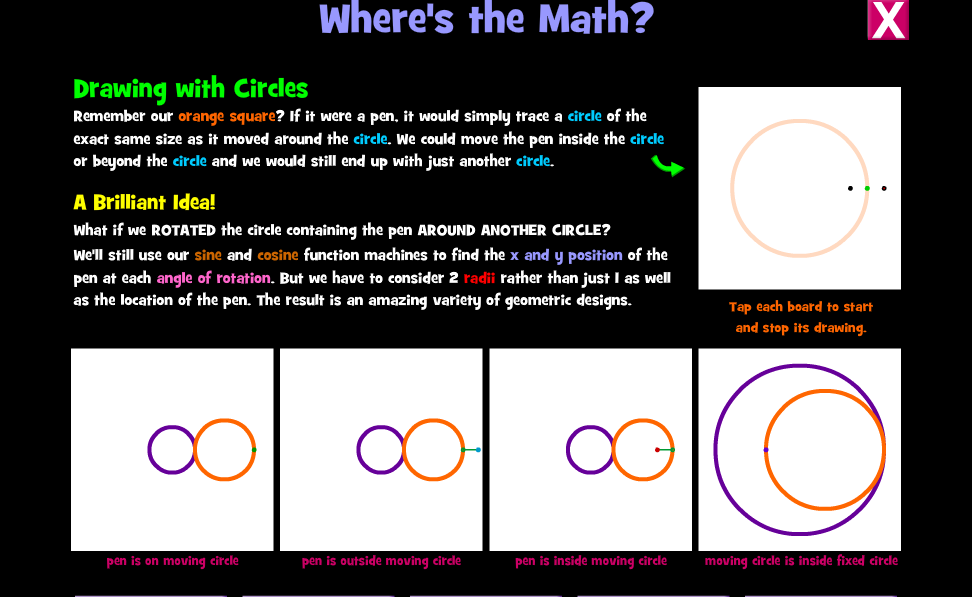
Τι λέτε όμως να γυρίσουμε στο αρχικό μας σημείο; Πάμε ξανά να δούμε τους κύκλους μας και γιατί όχι ......να αρχίσουμε να τους χαλάμε. Κάντε κλικ στο μοβ πλαίσιο: Drawing with Circles και θα δείτε το παρακάτω περιβάλλον:
|
Όπως μας λέει , φανταστείτε στον κύκλο με το πορτοκαλί τετραγωνάκι (βλέπε διπλανή εικόνα ) να υπήρχε ένας μαρκαδόρος που θα μπορούσε να γράφει με πολλά χρώματα ..... δε νομίζω ότι θα ήταν και πολύ εντυπωσιακό , αφού θα διέγραφε κάθε φορά έναν σταθερό , πολύχρωμο κύκλο , χωρίς να προκαλεί το ενδιαφέρον μας. Ωραία λοιπόν , πάμε να κάνουμε τις παρεμβάσεις ώστε να δώσουμε λίγο ενδιαφέρον στη δραστηριότητα , ας έχουμε τη δυνατότητα να μεταβάλουμε τη θέση του μαρκαδόρου μέσα ή έξω από τον κύκλο. Τι λέτε τώρα είναι αρκετό για να φτιάξουμε τα εντυπωσιακά σχέδια που είδατε πιο πάνω; Μπα δε νομίζω το μόνο που θα καταφέρναμε θα ήταν να φτιάχνονται κύκλοι με διαφορετικές ακτίνες. Νομίζω ότι πρέπει να σκεφτούμε κάτι διαφορετικό και αυτό είναι η περιστροφή ενός κύκλου γύρω από έναν άλλον. Πράγματι αν κάνετε κλικ σε κάθε μία από τις 4 πιο πάνω εικόνες στα λευκά τετράγωνα και θα δείτε μερικούς από τους εκατομμύρια σχεδιασμούς που προκύπτουν . Είναι νομίζω ώρα να σας αφήσω και να ενεργήσετε μόνοι σας , περιμένω εδώ σχόλια και εντυπώσεις ...και γιατί όχι και φωτογραφίες από τα σχέδια που δημιουργήσατε.
Καλή διασκέδαση. |