Mαθήματα skate από έναν επαγγελματία ...Προτείνω να πατήσετε το play και στη συνέχεια pause ώστε να κατέβει ολόκληρο το video και να το απολαύσετε . Μέχρι τότε διαβάστε το παρακάτω κόμιξ, που έφτιαξα για τις εξισώσεις 2ου βαθμού.
Εξισώσεις 2ου βαθμού( WolframAlpha )
Στην εικόνα βλέπουμε την γενική μορφή ενός τριωνύμου 2ου βαθμού , οπότε απαραίτητη προϋπόθεση είναι το (a) να είναι διάφορο του μηδενός. Για σκεφτείτε τι θα γινόταν αν ήταν το a=0.
Να ξέρετε ότι το τριώνυμο 2ου βαθμού έχει το πολύ 2 ρίζες (λύσεις) , δηλ. 2 τιμές για το χ , που επαληθεύουν την εξίσωση (ισότητα). Αυτό θα γίνει κατανοητό όταν θα αναφέρουμε την παραγοντοποίηση παραστάσεων και ειδικότερα τριωνύμου 2ου βαθμού.
Στις σημειώσεις που θα ανεβάσω θα διακρίνω την επίλυσή του σε 3 περιπτώσεις, όπου αρχικά θα έχουμε τα a,b,c διάφορα του μηδενός , στη συνέχεια θα έχουμε το (b) ίσο με το μηδέν και τέλος το (c).
Για να έχουμε όμως, ολοκληρωμένη εικόνα της εξίσωσης 2ου βαθμού, θα πρέπει να κάνουμε αναφορά στις συναρτήσεις και ειδικότερα στην παραβολή , αλλά αυτά θα ανέβουν σιγά σιγά , χωρίς άγχος.
Να ξέρετε ότι το τριώνυμο 2ου βαθμού έχει το πολύ 2 ρίζες (λύσεις) , δηλ. 2 τιμές για το χ , που επαληθεύουν την εξίσωση (ισότητα). Αυτό θα γίνει κατανοητό όταν θα αναφέρουμε την παραγοντοποίηση παραστάσεων και ειδικότερα τριωνύμου 2ου βαθμού.
Στις σημειώσεις που θα ανεβάσω θα διακρίνω την επίλυσή του σε 3 περιπτώσεις, όπου αρχικά θα έχουμε τα a,b,c διάφορα του μηδενός , στη συνέχεια θα έχουμε το (b) ίσο με το μηδέν και τέλος το (c).
Για να έχουμε όμως, ολοκληρωμένη εικόνα της εξίσωσης 2ου βαθμού, θα πρέπει να κάνουμε αναφορά στις συναρτήσεις και ειδικότερα στην παραβολή , αλλά αυτά θα ανέβουν σιγά σιγά , χωρίς άγχος.
|
Παραγοντοποίηση και γραφική παράσταση Τριωνύμου
Προς το παρόν , παρακάτω σας έχω μία ακόμη εφαρμογή του WolframAlpha σχετικά με την παραγοντοποίηση του τριωνύμου , αλλά και την γραφική του παράσταση . Δεν έχετε παρά να βάλετε τους συντελεστές του τριωνύμου και να πατήσετε Submit. Προσοχή , αν το τριώνυμο δεν έχει πραγματικές ρίζες (Δ<0) , η εφαρμογή το παραγοντοποιεί , βρίσκοντας τις μιγαδικές ρίζες . Τους μιγαδικούς αριθμούς μπορείτε να τους γνωρίσετε εδώ. |
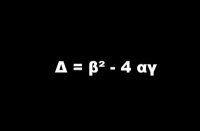
Πριν διαβάσετε τις σημειώσεις , καλό είναι να δείτε το παρακάτω video όπου βλέπουμε πως προκύπτει ο τύπος της Διακρίνουσας και οι ρίζες του τριωνύμου όταν αυτή είναι θετική ή μηδέν. Προσοχή, στη ξένη βιβλιογραφία η διακρίνουσα δεν συμβολίζεται με Δ , παρά μόνο γράφεται με την γνωστή της έκφραση. Το παρακάτω video είναι ένα από τα πολλά που έχει δημιουργήσει ο Salman kchan και η ομάδα του. Το έργο, που έχουν παρουσιάσει μέχρι στιγμής είναι εντυπωσιακό. Αμέτρητα video για όλους τους τομείς των μαθηματικών και όχι μόνο θα βρείτε στην ιστοσελίδα τους , που παρουσιάζω στα LINKS του COMMONMATHS.
Συνοπτικό Φυλλάδιο με τις 2ο βάθμιες εξισώσεις.
Τελευταία ενημέρωση 16 Μαρτίου 2016
Για να το κατεβάσετε σε μορφή PDF πατήστε εδώ .
Εδώ θα βρείτε μία μεγάλη ποικιλία από εφαρμογές θετικών επιστημών . Είναι μία αξιόλογη προσπάθεια από το University of Colorado , να φέρει το εργαστήριο στον Η/Υ μας. Η ιστοσελίδα είναι μεταφρασμένη και στα Ελληνικά , μιας και οι εκπαιδευτικοί Γιάννης Κασκαμανίδης, Βαγγέλης Κολτσάκης, Γιάννης Λευκός και Κωστής Χαλκιαδάκης προσφέρθηκαν να στηρίξουν τη προσπάθεια αυτή. Ανάλογα με τα θέματα, που θα ασχολούμε στο Comonmaths , θα ανεβάζω και τις κατάλληλες εφαρμογές.
Παρακάτω βλέπετε τη γενική μορφή μιας πολυωνυμικής συνάρτησης μέχρι 2ου βαθμού.Έχετε τη δυνατότητα να μεταβάλλετε τους συντελεστές του πολυωνύμου.Πειραματιστείτε και θα επανέλθω .
Παρακάτω βλέπετε τη γενική μορφή μιας πολυωνυμικής συνάρτησης μέχρι 2ου βαθμού.Έχετε τη δυνατότητα να μεταβάλλετε τους συντελεστές του πολυωνύμου.Πειραματιστείτε και θα επανέλθω .
