Το top 10 της euroleague 2013-2014 . Για να δείτε το video χωρίς διακοπές πατήστε το play και ύστερα το pause , για να κατέβει . Μέχρι τότε γιατί δεν ρίχνετε μια ματιά στους μιγαδικούς αριθμούς πιο κάτω ;
Πατήστε παρακάτω πάνω στον καταιγισμό ιδεών (brain storming) για να το δείτε σε μεγέθυνση.
Μιγαδικοί Αριθμοί( WolframAlpha) NEW : 1000 ΑΣΚΗΣΕΙΣ ΠΙΟ ΚΑΤΩ
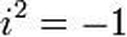
Οι μιγαδικοί αριθμοί δημιουργήθηκαν από την προσπάθεια των Ιταλών μαθηματικών S.del Ferro και Ν. Tartaglia να βρουν αναλυτικές λύσεις σε κυβικές εξισώσεις. Η διαδικασία επίλυσης τέτοιων εξισώσεων απαιτεί ενδιάμεσους υπολογισμούς, οι οποίοι μπορεί να περιλαμβάνουν τετραγωνικές ρίζες αρνητικών αριθμών, ακόμα κι όταν η λύση είναι πραγματικός αριθμός. Ο J.Hadamard , o οποίος το 1896 απέδειξε με χρήση της μιγαδικής ανάλυσης το θεώρημα των πρώτων αριθμών , έγραψε ότι :
''Ο συντομότερος δρόμος ανάμεσα σε δύο αλήθειες στο πεδίο των πραγματικών περνά μέσα απο το πεδίο των μιγαδικών.''
Αρκετά όμως με την ιστορία των Μαθηματικών , που όσο και να γράφεις, ποτέ δεν είναι αρκετό.
Στα δικά μας τώρα , έχω έτοιμες τις σημειώσεις των Μιγαδικών Αριθμών.
Το αρχείο σε μορφή PDF είναι σε αυτή τη σελίδα: ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΑΡΙΘΜΩΝ , που έχει κωδικό πρόσβασης. Ο κωδικός μπορεί να δοθεί , κατόπιν συνεννόησης . Η επικοινωνία μπορεί να γίνει στην ειδική φόρμα του site.
Στις σημειώσεις που παρουσιάζω πιο κάτω , θα βρείτε όλη τη θεωρία σε μορφή ερωτήσεων-απαντήσεων και παρουσιάζονται όλα τα 1α θέματα των πανελλαδικών εξετάσεων. Είναι ένα χρήσιμο φυλλάδιο, το οποίο θα σας βοηθήσει να μάθετε τη θεωρία των μαθηματικών γρήγορα και εύκολα, δεν αντικαθιστά το σχολικό βιβλίο , αλλά σας βοηθάει να το κατανοήσετε 100%.
''Ο συντομότερος δρόμος ανάμεσα σε δύο αλήθειες στο πεδίο των πραγματικών περνά μέσα απο το πεδίο των μιγαδικών.''
Αρκετά όμως με την ιστορία των Μαθηματικών , που όσο και να γράφεις, ποτέ δεν είναι αρκετό.
Στα δικά μας τώρα , έχω έτοιμες τις σημειώσεις των Μιγαδικών Αριθμών.
Το αρχείο σε μορφή PDF είναι σε αυτή τη σελίδα: ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΑΡΙΘΜΩΝ , που έχει κωδικό πρόσβασης. Ο κωδικός μπορεί να δοθεί , κατόπιν συνεννόησης . Η επικοινωνία μπορεί να γίνει στην ειδική φόρμα του site.
Στις σημειώσεις που παρουσιάζω πιο κάτω , θα βρείτε όλη τη θεωρία σε μορφή ερωτήσεων-απαντήσεων και παρουσιάζονται όλα τα 1α θέματα των πανελλαδικών εξετάσεων. Είναι ένα χρήσιμο φυλλάδιο, το οποίο θα σας βοηθήσει να μάθετε τη θεωρία των μαθηματικών γρήγορα και εύκολα, δεν αντικαθιστά το σχολικό βιβλίο , αλλά σας βοηθάει να το κατανοήσετε 100%.
Για να το κατεβάσετε πατήστε εδώ.
Πιο κάτω θα βρείτε 1120 ασκήσεις μιγαδικών (6η έκδοση ) , που καλύπτουν σχεδόν όλες τις μεθοδολογίες. Η συλλογή των παρακάτω ασκήσεων είναι προϊόν μίας αξιόλογης προσπάθειας ενός μέλους (zorba_the_freak) του forum του Mathematica.gr το οποίο και ευχαριστώ πολύ. Δυστυχώς δεν έχω το δικαίωμα να σας δώσω τη δυνατότητα να τις κατεβάσετε στον υπολογιστή σας.
Για να το κατεβάσετε πατήστε εδώ.
Περιμένω σχόλια εδώ.
Στο παρακάτω video μπορούμε να παρακολουθήσουμε μια συνοπτική ιστορική παρουσίαση των μιγαδικών αριθμών και όχι μόνο . Πριν διαβάσετε τις σημείωσεις και πριν δείτε τα μαθηματικά video , καλό είναι να μπείτε στο νόημα των μιγαδικών σιγά σιγά . Καλή διασκέδαση .
|
|
Κάτι σαν υπότιτλοι ...
|
Πράξεις με μιγαδικούς.
Παρακάτω σας έχω μία εφαρμογή από το WolframAlpha , που παρουσιάζω στα Links . Σε αυτήν την εφαρμογή
μπορείτε να τσεκάρετε τις πραξεις σας στους μιγαδικούς αριθμούς .
Περιμένω σχόλια εδώ.
μπορείτε να τσεκάρετε τις πραξεις σας στους μιγαδικούς αριθμούς .
Περιμένω σχόλια εδώ.
Τώρα θα δείτε μια σειρά 10λεπτων video από το γνωστό , πλέον , site KHANacademy , που παρουσιάζω στα Links.
Complex number (part 1)
Εδώ θα δούμε πως ορίζονται οι μιγαδικοί αριθμοί, καθώς και οι πράξεις αυτών πρόσθεση , αφαίρεση και πολλαπλασιασμός.
Complex conjugates example(συζυγείς μιγαδικοί)
Στη συνέχεια θα ορίσουμε τον συζυγή μιγαδικό του z=α+βi.
Complex number (part 2)
Στο παρακάτω video παρουσιάζεται η διαίρεση δύο μιγαδικών.
Δυνάμεις του i
Στα παρακάτω 2 dideo παρουσιάζονται οι δυνάμεις του i.
Περιμένω σχόλια εδώ
