Origami πυραμίδα

Αυτή τη φορά δεν θα σας δυσκολέψω καθόλου, δηλαδή έτσι νομίζω, αφού η κατασκευή Origami Πυραμίδα είναι αρκετά εύκολη και γρήγορη. Μαζί με την άλλη κατασκευή του Κύβου (αρκετά δύσκολη θα έλεγα ), που μπορείτε να δείτε εδώ, έχετε τη δυνατότητα να επεξεργαστείτε άμεσα δύο από τα βασικά στερεά της Στερεομετρίας. Σύντομα θα ακολουθήσουν και τα υπόλοιπα.
Εδώ είναι μία άλλη κατασκευή με τρεις ίδιες Πυραμίδες, που συνθέτουν έναν Κύβο.
Εδώ ένα άρθρο σχετικά με τον όγκο της Πυραμίδας.
Εδώ ένα φύλλο εργασίας για την κατασκευή της Πυραμίδας του Χέοπα , υπό κλίμακα 1:1000 και η μέτρηση του ύψους της . (ΘΑΛΗΣ)
Μετά το video, πιο κάτω, μπορείτε να δείτε και τη Γεωμετρία,  που κρύβεται πίσω από την κατασκευή της Πυραμίδας .

---

Περιμένω σχόλια εδώ.

Ύστερα από σχόλιο του καλού συναδέλφου Κώστα Λαμπρινίδη,  η πιο πάνω πυραμίδα κρύβει κάποια μυστικά που θα παρουσιάσω ευθείς αμέσως.
Οι 4 έδρες της Πυραμίδας είναι ισοσκελή τρίγωνα, οπότε αυτό που καταφέραμε,  είναι με τη δίπλωση του χαρτιού να σχηματίσουμε 60 μοιρών γωνία.
Ο Κώστας Λαμπρινίδης στο παρακάτω video παρουσιάζει την απόδειξη.

Πάμε όμως να δούμε την πιο πάνω απόδειξη πως εφαρμόζεται στο video της κατασκευής.

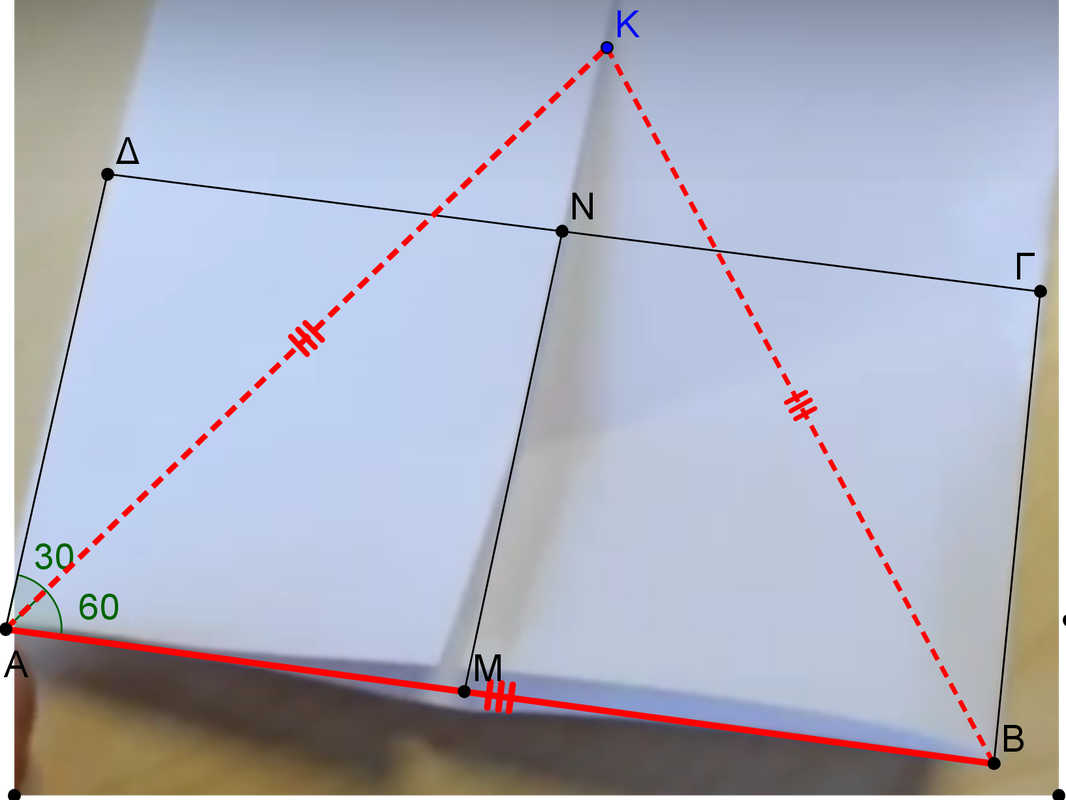
Το ΜΝ είναι η μεσοκάθετος του ΑΒ, άρα κάθε σημείο της θα ισαπέχει από τα άκρα του ΑΒ. Συνεπώς  ΚΑ=ΚΒ. Τώρα θα μου πείτε πως προέκυψε το Κ . Το σημείο Κ προκύπτει από τη δίπλωση του χαρτιού, που βλέπετε στην 2η εικόνα.

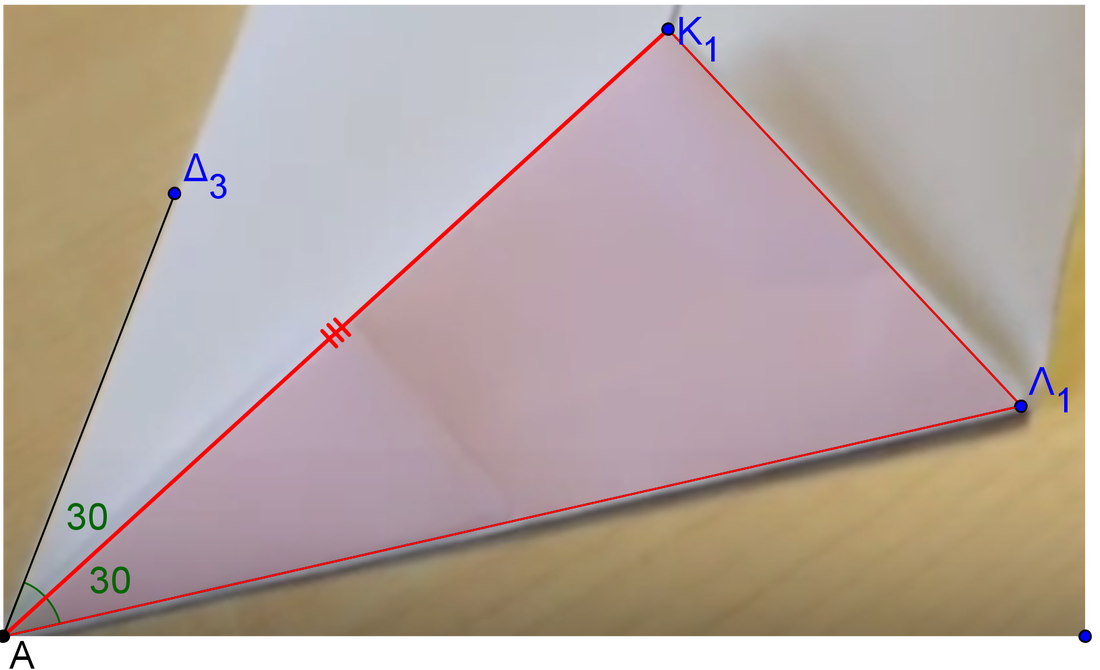
Σηκώνουμε την κορυφή Β, που βλέπετε στην 1η εικόνα και διπλώνουμε το χαρτί ώστε να καταλήξει στη μεσοκάθετο ΜΝ του ΑΒ. Προσοχή κατά τη δίπλωση, θα πρέπει να δημιουργηθεί ένα τρίγωνο ΑΚΛ ( βλέπε 2η εικ. ). Το τμήμα ΑΚ που δημιουργείται  είναι το ΑΒ , που βλέπετε στην 1η εικόνα για αυτό και ΚΑ=ΑΒ. Άρα το τρίγωνο ΑΚΒ της 1ης εικόνας είναι ισόπλευρο, συνεπώς η γωνΚΑΒ=60 μοίρες=> γωνΔΑΚ=90-60=30  μοίρες.
Το ότι η γωνΚΑΛ=30 μοίρες, προκύπτει από τη δίπλωση της γωνΚΑΒ που βλέπετε στην 1η εικόνα, αφού είναι 60 μοιρών και διπλώνεται στη μέση και έτσι προκύπτει η γωνία των 30 μοιρών.

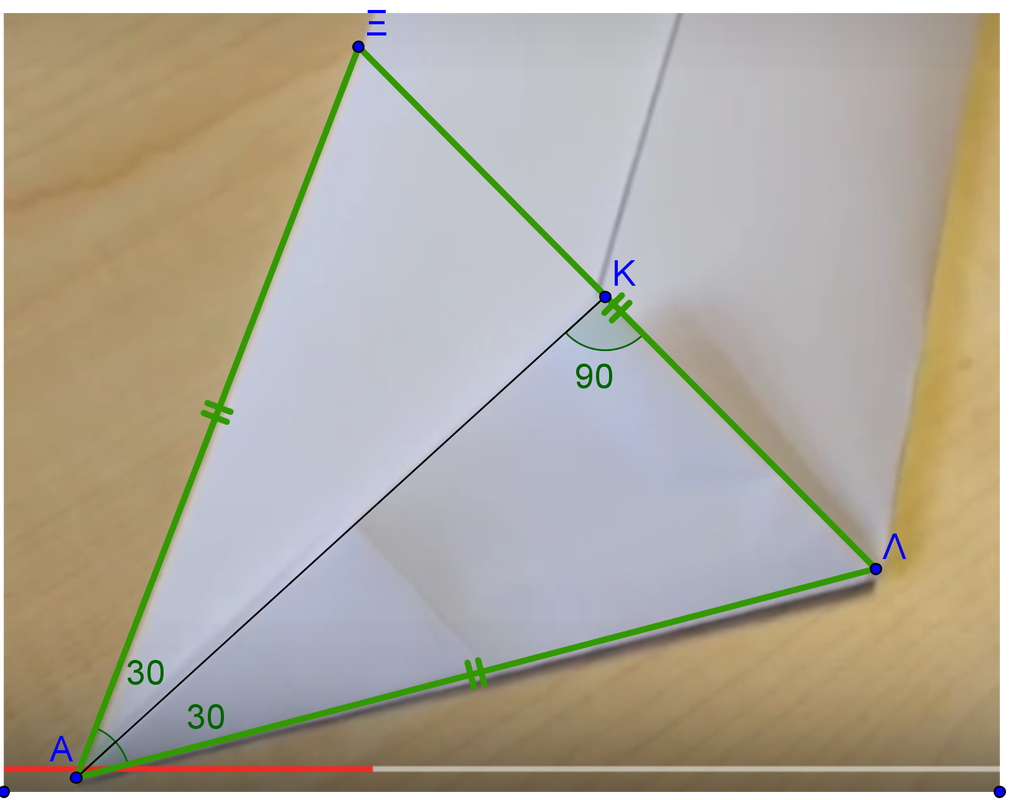
Κάντε λίγο υπομονή τελειώνουμε. Στο τρίγωνο ΞΑΛ η ΑΚ είναι διχοτόμος αλλά και ύψος , αφού γωνΚ=90 μοίρες. Άρα ΑΚ=διχοτόμος+ύψος=> τριγΞΑΛ=ισοσκελές με ΑΞ=ΑΛ=> γωνΞ=γωνΛ=60 μοίρες αφού η γωνία της κορυφής είναι γωνΞΑΛ=60 μοιρών. Οπότε το ΞΑΛ είναι ισόπλευρο.
Τελειώσαμε...επιτέλους. Καταφέραμε να δείξουμε ότι το ΞΑΛ είναι ισόπλευρο. Βλέποντας το video πιο προσεχτικά με γνώμονα το ισόπλευρο τρίγωνο ΞΑΛ δημιουργούμε και τα υπόλοιπα ισόπλευρα τρίγωνα, που θα αποτελέσουν τις έδρες της πυραμίδας μας.