Κάντε κλικ στην εικόνα.
Με τη βοήθεια του πιο πάνω καταιγισμού ιδεών , να ορίσετε τους τριγωνομετρικούς αριθμούς μέσω του ορθογωνίου τριγώνου και του τριγωνομετρικού κύκλου.
Τριγωνομετρικός Κύκλος
Το πρόβλημα με το σύστημα των αξόνων είναι ότι κάθε φορά για να υπολογίσουμε τους τριγωνομετρικούς αριθμούς μιας γωνίας είναι ότι πρέπει να υπολογίσουμε το (ρ) , όπως είδαμε στην 2η ενότητα , που εξαρτάται από τις συντεταγμένες του αντίστοιχου σημείου Μ(χ,y). Ποιό είναι λοιπόν το πλεονέκτημα του τριγωνομετρικού κύκλου;
Πριν απαντήσουμε πάμε να δούμε τον ορισμό του: <<Με κέντρο την αρχή Ο(0,0) ενός συστήματος συντεταγμένων και ακτίνα ρ=1 γράφουμε έναν κύκλο .Ο κύκλος αυτός λέγεται τριγωνομετρικός κύκλος>>
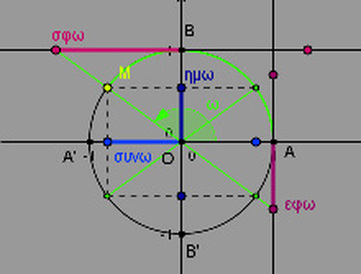
Όπως καταλαβαίνεται το πλεονέκτημά του είναι ότι το ρ=1 οπότε για οποιαδήποτε γωνία ω υπάρχει ένα μόνο σημείο του τριγωνομετρικού κύκλου Μ(χ,y) που απέχει από το Ο(0,0) απόσταση ίση με 1. Στους παρονομαστές λοιπόν των ημιτόνων και συνημιτόνων θα βάλουμε το 1 , με αποτέλεσμα το ημω=y και το συνω=χ . Όπως βλέπουμε και στο διπλανό σχήμα ο άξονας των χ (τετμημένων) ταυτίζεται με τον άξονα των συνημιτόνων (συνω) και ο άξονας των y (τεταγμένων) ταυτίζεται με τον άξονα τον άξονα των ημιτόνων (ημω).
Το παρακάτω video είναι κατατοπιστικό αν και είναι στα Αγγλικά . Προσοχή μη ξεχνάτε ότι sinθ=ημθ και cosθ=ημθ .0 καθηγητής που ακούγεται χρησιμοποιεί το ορθογώνιο τρίγωνο για τους ορισμούς των τριγωνομετρικών αριθμών, όπως τους παρουσιάσαμε και εμείς στην 1η ενότητα.
Πριν απαντήσουμε πάμε να δούμε τον ορισμό του: <<Με κέντρο την αρχή Ο(0,0) ενός συστήματος συντεταγμένων και ακτίνα ρ=1 γράφουμε έναν κύκλο .Ο κύκλος αυτός λέγεται τριγωνομετρικός κύκλος>>
Όπως καταλαβαίνεται το πλεονέκτημά του είναι ότι το ρ=1 οπότε για οποιαδήποτε γωνία ω υπάρχει ένα μόνο σημείο του τριγωνομετρικού κύκλου Μ(χ,y) που απέχει από το Ο(0,0) απόσταση ίση με 1. Στους παρονομαστές λοιπόν των ημιτόνων και συνημιτόνων θα βάλουμε το 1 , με αποτέλεσμα το ημω=y και το συνω=χ . Όπως βλέπουμε και στο διπλανό σχήμα ο άξονας των χ (τετμημένων) ταυτίζεται με τον άξονα των συνημιτόνων (συνω) και ο άξονας των y (τεταγμένων) ταυτίζεται με τον άξονα τον άξονα των ημιτόνων (ημω).
Το παρακάτω video είναι κατατοπιστικό αν και είναι στα Αγγλικά . Προσοχή μη ξεχνάτε ότι sinθ=ημθ και cosθ=ημθ .0 καθηγητής που ακούγεται χρησιμοποιεί το ορθογώνιο τρίγωνο για τους ορισμούς των τριγωνομετρικών αριθμών, όπως τους παρουσιάσαμε και εμείς στην 1η ενότητα.
Πάμε όμως να δούμε αναλυτικά τον τριγωνομετρικό κύκλο. (Εδώ θα βρείτε τις σημειώσεις σε μορφή PDF)
ΕΦΑΡΜΟΓΗ GEOGEBRA
Αφού διαβάσετε τις σημειώσεις, δείτε και την παρακάτω εφαρμογή του PHET στον τριγωνομετρικό κύκλο.
Το πλεονέκτημα του λογισμικού είναι ότι μπορείτε με την βοήθεια του mouse να μετακινείτε το σημείο στην περιφέρεια του κύκλου και να βγάζετε εύκολα συμπεράσματα. Π.χ. αν τοποθετήσετε το σημείο στα 4 σημεία του ορίζοντα θα δείτε τους τριγωνομετρικούς αριθμούς των 0 , 90 , 180 , 270 , 360 μοιρών και όχι μόνο. Δοκιμάστε το και επαληθεύστε τα νούμερα με τον πίνακα των τριγωνομετρικών αριθμών.
Το πλεονέκτημα του λογισμικού είναι ότι μπορείτε με την βοήθεια του mouse να μετακινείτε το σημείο στην περιφέρεια του κύκλου και να βγάζετε εύκολα συμπεράσματα. Π.χ. αν τοποθετήσετε το σημείο στα 4 σημεία του ορίζοντα θα δείτε τους τριγωνομετρικούς αριθμούς των 0 , 90 , 180 , 270 , 360 μοιρών και όχι μόνο. Δοκιμάστε το και επαληθεύστε τα νούμερα με τον πίνακα των τριγωνομετρικών αριθμών.
