Ορθοκανονικό σύστημα αξόνων
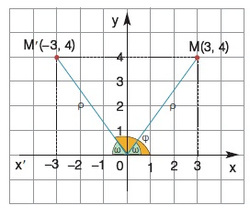
Πάμε όμως τώρα να ορίσουμε τους τριγωνομετρικούς αριθμούς με τη βοήθεια ενός ορθοκανονικού συστήματος αξόνων. Ο λόγος που το κάνουμε είναι οτι στο ορθογωνίο τρίγωνο συναντάμε μόνο οξείες γωνίες, ενώ με το σύστημα αξόνων μπορούμε να ασχοληθούμε με οποιαδήποτε γωνία.
Όπως βλέπουμε στο σχήμα για κάθε σημείο Μ(χ,y) του επιπέδου αντιστοιχεί και μία γωνία φ και το αντίστροφο. Αν το σημείο Μ είναι στο 1ο τεταρτημόριο η αντίστοιχη γωνία θα είναι οξεία , αν είναι στο 2ο τότε προκύπτει αμβλεία γωνία , στο 3ο προκύπτει γωνία που θα είναι πάνω από 180 μοίρες και λιγότερο από 270 μοίρες, ενώ στο 4ο πάνω από 270 μοίρες και λιγότερο από 360 μοίρες. Βέβαια κανείς δεν μας εμποδίζει να κάνουμε μια πλήρης περιστροφή (360 μοίρες) και να συνεχίσουμε όσο θέλουμε διαγράφοντας έτσι μια γωνία μεγαλύτερη των 360 μοιρών. Ωστόσο το τελικό και απόλυτο εργαλείο για την τριγωνομετρία θα είναι ο ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΣ ΚΥΚΛΟΣ που θα τον μελετήσουμε στην επόμενη ενότητα . Αλλά ας δούμε εδώ συνοπτικά πως ορίζονται οι τριγωνομετρικοί αριθμοί με το σύστημα αξόνων.
Όπως βλέπουμε στο σχήμα για κάθε σημείο Μ(χ,y) του επιπέδου αντιστοιχεί και μία γωνία φ και το αντίστροφο. Αν το σημείο Μ είναι στο 1ο τεταρτημόριο η αντίστοιχη γωνία θα είναι οξεία , αν είναι στο 2ο τότε προκύπτει αμβλεία γωνία , στο 3ο προκύπτει γωνία που θα είναι πάνω από 180 μοίρες και λιγότερο από 270 μοίρες, ενώ στο 4ο πάνω από 270 μοίρες και λιγότερο από 360 μοίρες. Βέβαια κανείς δεν μας εμποδίζει να κάνουμε μια πλήρης περιστροφή (360 μοίρες) και να συνεχίσουμε όσο θέλουμε διαγράφοντας έτσι μια γωνία μεγαλύτερη των 360 μοιρών. Ωστόσο το τελικό και απόλυτο εργαλείο για την τριγωνομετρία θα είναι ο ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΣ ΚΥΚΛΟΣ που θα τον μελετήσουμε στην επόμενη ενότητα . Αλλά ας δούμε εδώ συνοπτικά πως ορίζονται οι τριγωνομετρικοί αριθμοί με το σύστημα αξόνων.
